Resolvendo o problema do Caixeiro Viajante utilizando o algoritmo de enxame de abelhas ABC

abelhas produtoras de mel

Algoritmo de Enxame de abelhas ideia princípal

Inspirado pelo comportamento inteligente de forrageamento (i.e., busca por alimento) dos enxames de abelhas produtoras de mel, o algoritmo de colônia de abelhas (ABC)(do inglês, Artificial Bee Colony Algorithm) é uma meta-heurística baseada em população (KARABOGA et al. ,2014). O ABC foi proposto inicialmente por Karaboga (2005) para solucionar problemas de otimização contínua e posteriormente também foi adaptado para problemas de domínio discreto ( KARABOGA , 2005; KARABOGA; BASTURK , 2007, 2008; KARABOGA ,2009; KARABOGA; AKAY , 2009; KARABOGA et al. , 2014).

Karaboga (2005) descreve em seu trabalho que o algoritmo ABC é composto por três tipos de abelhas, sendo elas: empregadas, espectadoras e a exploradora. A função da abelha empregada é a de explorar fontes de alimentos em sua vizinhança (i.e., busca local). A abelha que fica na colmeia esperando para tomar a decisão de qual fonte de alimento escolher para explorar é conhecida como espectadora (i.e., busca local). A abelha que sai a procura de novas fontes de alimentos de forma aleatória é a exploradora (i.e., busca global).

A colmeia de abelhas do algoritmo ABC é composta por 50% de abelhas empregadas e espectadoras e 1 abelha exploradora. No processo de forrageamento do ABC inicialmente as abelhas empregadas são enviadas para as fontes de alimento para a coleta de néctar. Depois de recolher o alimento ela volta para a colmeia e compartilha as informações da localização dessa fonte de alimento para a abelha espectadora. Esse processo de comunicação entre essas abelhas é conhecido como dança do requebrado (do inglês, wiggle dance). Então, após uma fonte de alimento se esvaziar a abelha espectadora que era designada aquela fonte de alimento se torna uma abelha exploradora e sai para fora da colmeia em busca de novas fontes de alimento.

Com base no contexto supracitado, Karaboga (2005) desenvolveu a ideia do algoritmo ABC. Para mais detalhes eu sugiro que você faça a leitura do artigo do profº Karaboga de 2005.

Antes de iniciar os processos a serem apresentados a seguir, se você desejar, seria interessante o uso de um ambiente virtual fechado. Para isso você pode consultar esse link para o artigo para ver como utilizar um ambiente virtual fechado em projetos python. Se não, pode continuar a leitura.

Aplicando os conceitos do algoritmo ABC no problema do CV

O problema do Caixeiro Viajante (CV) representa a ideia de um CV que tem de visitar um conjunto de cidades sem repetir nenhuma delas de modo que ele retorne a cidade inicial por meio da menor distância possível.

O primeiro passo para trabalhar com o problema do CV é realizar a leitura das coordenadas das cidades e gerar a tabela de distâncias referente a essas cidades.

Antes de começar o passo a passo, é importante salientar que será utilizado no decorrer do artigo a linguagem de programação python na versão 3 e será necessário instalar algumas bibliotecas sendo elas a numpy e a matplotlib. Caso você não as tenha instaladas no seu computador a seguir é ilustrado um exemplo dos comandos necessários para instalar as bibliotecas mencionadas.

    Abra seu terminal e digite os comandos:
    pip install numpy
    pip install matplotlib

Depois de instalar as bibliotecas utilizadas faça o seguinte:

Abra seu editor de texto favorito e crie o seguinte arquivo rafael5.txt;
Em seguida salve o seguinte conteudo dentro do arquivo criado:

No bloco acima, a primeira coluna representa a cidade, a segunda coluna a coordenada x da cidade e a terceira coluna a coordenada y da cidade;
No meu caso, eu criei um diretório (i.e., uma pasta) chamado “tsp-instancias” e dentro dele eu coloquei o arquivo rafael5.txt;
No mesmo nível do diretório “tsp-instancias” crie um arquivo python chamado abc.py.

├── abc.py
└── tsp-instancias
    └── rafael5.txt

No arquivo abc.py você irá inserir os códigos apresentados no decorrer do artigo para implementar o algoritmo ABC.

Para realizar a leitura dos dados por meio de um arquivo externo (i.e., nosso arquivo rafael5.txt que tem os dados do problema do cv), utiliza-se a seguinte forma a baixo:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
    import numpy as np #biblioteca que facilita o armazenamento e o acesso a matrizes e vetores de forma otimizada além de proporcinar métodos que facilitam a manipulação dos dados
    import math # fornece funcões matemáticas
    import matplotlib.pyplot as plt #facilita e prove a geração de gráficos em python

    instancia     = 'tsp-instancias/rafael5.txt'
    cidades       = np.genfromtxt(instancia, delimiter=' ', usecols=(0))

    coordenadas_x = np.genfromtxt(instancia, delimiter=' ', usecols=(1))
    coordenadas_y = np.genfromtxt(instancia, delimiter=' ', usecols=(2))

    numero_cidades = len(cidades)

    fig, ax = plt.subplots()

    for i, txt in enumerate(cidades):
        ax.annotate(int(txt), (coordenadas_x[i], coordenadas_y[i]))

        plt.xlabel('Coordenadas X')
    plt.ylabel('Coordenadas Y')
    plt.title('Coordenadas das cidades utilizadas no CV')

    plt.plot(coordenadas_x,coordenadas_y,'ro')
    plt.show()

Para gerar a tabela de que representa a distância gasta entre as cidades utiliza-se a função a seguir:

1
2
3
4
5
6
7
8
9
10
11
12
    #com os dados das coordenadas das cidades, aplicar a formula que calcula a distância (e.g., distância eucliana) entre as cidades para todas as cidades da cidade 1 até a cidade D!
    def distancia_euclidiana(x,y):
        distancias = np.zeros([numero_cidades,numero_cidades])
        for i in range(len(x)):
            for j in range(len(y)):
                #aplicando a distancia eucliana nas cidades i e j nas suas respectivas coordenadas x e y
                distancias[i][j] = math.sqrt( math.pow( (x[i]-x[j]+y[i]-y[j]), 2) ) #calcula a distância da cidade i para a cidade j
        return distancias
    #aqui ficaram armazenadas as distâncias que o cv vai gastar de uma cidade para outra depois de aplicar a distância euclidiana
    distancias = distancia_euclidiana(coordenadas_x,coordenadas_y)

print(distancias) #imprimindo na tela a matriz gerada com as distâncias da cidade 1 até a cidade D

Com os dados básicos do problema do CV, agora já é possível começar a pensar no algoritmo ABC de fato para realizar a otimização do problema.

Fluxograma do algoritmo ABC

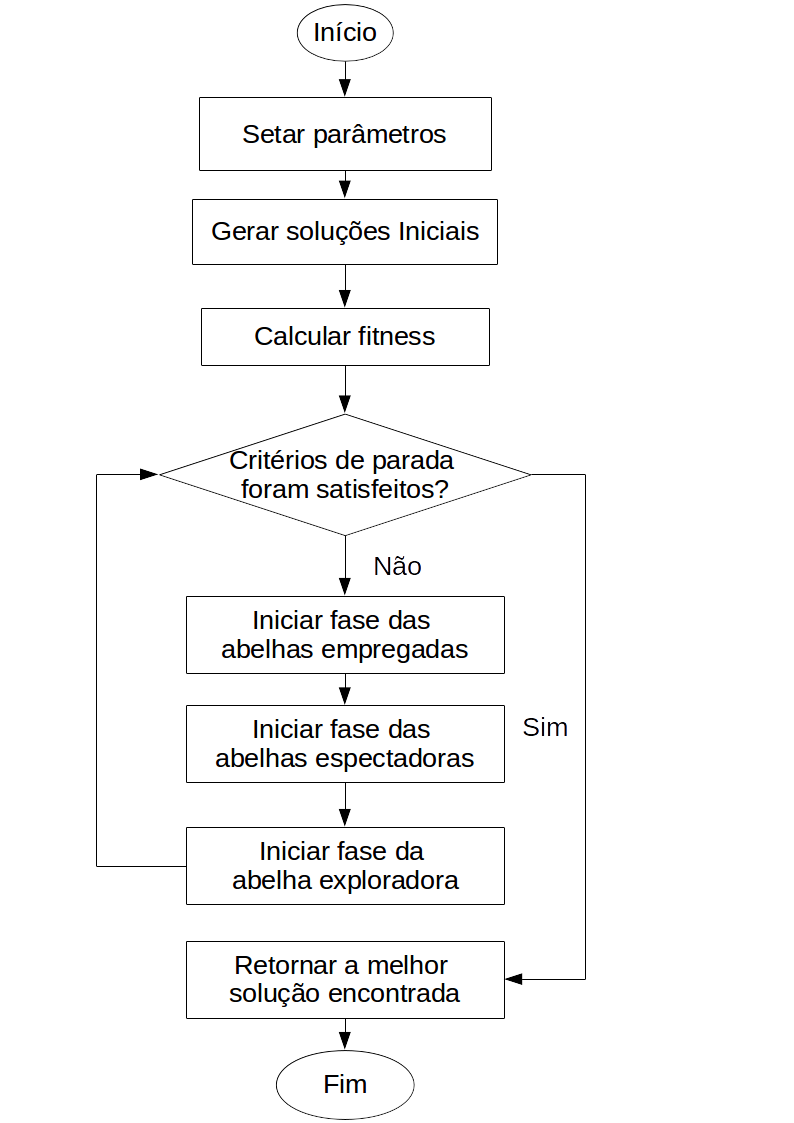
abelhas produtoras de mel

Modelagem da Solução (i.e., representação das variáveis de decisão do problema estudado)

A modelagem da solução é a forma com a qual seu algoritmo ABC representa as variáveis de decisão do problema de otimização em questão. No caso do CV a representação utilizada será a seguinte:

Cada abelha terá como solução uma sequência de cidades e.g., (1, 2, 3, …, até N) sendo que N representa a quantidade de cidades do nosso problema/exemplo e nesse caso, N=5 de modo que elas não se repitam. O fato delas não se repetirem é considerado como uma restrição do problema em questão.

SETAR OS PARÂMETROS DO ABC

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
### SETAR PARÂMETROS INICIO ###
#Configuração/Parametrização do algoritmo ABC
tamanhoDaColonia = 10 # tamanho total da colônia de abelhas (empregadas e espectadoras)
metadeDaColonia = tamanhoDaColonia/2 #referente ao tamanho da metade da colônia de abelhas
numeroDeTentativas = 10 # número de tantivas que relacionadas a uma solução poder ser melhorada
D = numero_cidades #dimensionalidade do problema em questão ou seja, quantidade de váriaveis de decisão
numeroDeCiclosDeForrageamento = 50 #número de iterações realizados pelas abelhas na colmeia ou ciclo de trabalho delas na busca por mel
numeroDeExecucoes = 10 #número de execuções realizadas pelo algoritmo ABC

colonia = np.zeros([metadeDaColonia,D], dtype=int) #criação da colonia de abelhas onde cada linha representa uma abelha e as colunas os locus de mel referentes as variavéis de decisão do problema abordado pelo ABC
tentativas = np.zeros([metadeDaColonia]) #array que armazenara as tentativas das fontes de alimento evoluirem referente a cada abelha da colmeia
fitnessDaColonia = np.zeros([metadeDaColonia]) #array que armazenara a qualidade das fontes de alimento das abelhas da colmeia


melhorSolucao = np.zeros([D], dtype=int) #melhor solução atual
melhorFitness = 0 #valor de fitness da melhor solução atual

melhoresSolucoes = np.zeros([numeroDeExecucoes,D], dtype=int) #matriz com as melhores soluções encontradas em cada execução do ABC
melhoresFitness  = np.zeros([numeroDeExecucoes]) #array referente as melhores soluções
### SETAR PARÂMETROS FIM ###

FUNÇÃO DE APTIDÃO/FITNESS UTILIZADA PARA AVALIAR AS SOLUÇÕES DO ABC NO PROBLEMA DO CV

No problema do CV a função de fitness avalia a sequência das cidades representada por cada solução gerenciadas por cada abelha.

1
2
3
4
5
6
7
# função de fitness utilizada para mensurar a qualidade das soluções
def fitness(solucao,distancias):
    valorDoFitness = 0
    for i in range(len(solucao)-1):
        valorDoFitness += distancias[solucao[i],solucao[i+1]]
    valorDoFitness += distancias[solucao[-1],solucao[0]] #retornando da ultima cidade para a cidade inicial
    return valorDoFitness

CRIAÇÃO DA POPULAÇÃO INICIAL DE ABELHAS DO ENXAME NO ABC PARA O PROBLEMA DO CV

Assim que as soluções iniciais são geradas elas são avaliadas para que se possa saber a qualidade da fonte de alimentos de cada abelha.

1
2
3
4
#gerar população inicial de abelhas
for i in range(metadeDaColonia):
    colonia[i,:] = np.random.permutation(D) #para cada abelha gerar um roteiro de cidades/variaveis de decisão
    fitnessDaColonia[i] = fitness(colonia[i],distancias) #calcular a aptidão/fitness de cada Abelha i

MÉTODO DE SELEÇÃO UTILIZADO NO ABC

Depois que todas as abelhas empregadas trabalham nas suas respectivas fontes de alimentos, um método de seleção é utilizado para selecionar uma abelha espectadora para melhorar cada solução de cada abelha empregada. Para isso, pode-se utilizar o método de Roleta Probabilística. Não existe apenas esse método e se você quiser pode pesquisar por outros e utilizá-los em seu lugar para ver o que acontece com o resultado gerado pelo ABC.

1
2
3
4
5
6
7
def selecaoPorRoleta(fitness): #Roleta probabilista refente as aptidoes/fitness da colonia de abelhas
    probs = fitness[:]/fitness.sum()
    escolhida = np.random.uniform(0,probs.sum(),1)
    for i in range(len(probs)):
        if probs[i] > escolhida:
            return i
    return -1

A TROCA SWAP É APENAS UM MÉTODO QUE ALTERA AS SOLUÇÕES/FONTES DE ALIMENTOS DAS ABELHAS DO ABC

1
2
3
4
5
6
7
8
def trocaSwap(novaSolucao):
    posicaoDeTrocas = np.random.randint(D, size=(2)) #gerando 2 posições aleatórias
    while posicaoDeTrocas[0] == posicaoDeTrocas[1]: #garantindo que os números gerados são diferentes
        posicaoDeTrocas = np.random.randint(D, size=(2))
    aux = novaSolucao[posicaoDeTrocas[0]]
    novaSolucao[posicaoDeTrocas[0]] = novaSolucao[posicaoDeTrocas[1]]
    novaSolucao[posicaoDeTrocas[1]] = aux
    return novaSolucao

A seguir é apresentado o fluxo do ABC do mesmo modo que no fluxograma supracitado nesse artigo:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#definir quem é a abelha com melhor fonte de alimento
melhorSolucao[:] = colonia[fitnessDaColonia.argmin()]
melhorFitness = fitnessDaColonia[fitnessDaColonia.argmin()]

for r in range(numeroDeExecucoes):
    #print("Execucao numero: %d" % (r))
    for iteracao in range(numeroDeCiclosDeForrageamento): #criterio de parada é quantidade de ciclos de forrageamento
        #print("Iteracao: %d" % (iteracao))
        #iniciar fase das abelhas empregadas
        for i in range(metadeDaColonia):
            #gerar uma perturbação na solucao da abelha i e verificar se essa nova solução é melhor que a velha
            novaSolucao = np.zeros([D], dtype=int)
            #aplicando o método simples de troca swap
            novaSolucao[:] = trocaSwap(colonia[i])
            #verificar se a nova solucao tem melhor aptidão que a velha solução/fonte de alimentos da abelha i
            if fitness(novaSolucao,distancias) < fitnessDaColonia[i]:
                colonia[i,:] = novaSolucao
                fitnessDaColonia[i] = fitness(novaSolucao,distancias)
                tentativas[i] = 0 # se a solução foi melhorada reseta o numero de tentativas dessa fonte de alimento
            else:
                tentativas[i] += 1 # se a solução da abelha i não melhorou o array de tentativas na posição i deve ser incrementado representando que a solução i não pode ser melhorada

        #iniciar fase das abelhas espectadoras
        for j in range(metadeDaColonia):   
            abelhaEmpregadaEscolhida = selecaoPorRoleta(fitnessDaColonia)
            while abelhaEmpregadaEscolhida == -1:
                abelhaEmpregadaEscolhida = selecaoPorRoleta(fitnessDaColonia)
            #gerar uma perturbação na solucao da abelha i e verificar se essa nova solução é melhor que a velha
            novaSolucao = np.zeros([D], dtype=int)
            #aplicando o método simples de troca swap na abelha empregada escolhida pelo método de seleção adotado
            novaSolucao[:] = trocaSwap(colonia[abelhaEmpregadaEscolhida])
            #verificar se a nova solucao tem melhor aptidão que a velha solução/fonte de alimentos da abelha i
            if fitness(novaSolucao,distancias) < fitnessDaColonia[i]:
                colonia[i,:] = novaSolucao
                fitnessDaColonia[i] = fitness(novaSolucao,distancias)
                tentativas[i] = 0 # se a solução foi melhorada reseta o numero de tentativas dessa fonte de alimento
            else:
                tentativas[i] += 1 # se a solução da abelha i não melhorou o array de tentativas na posição i deve ser incrementado representando que a solução i não pode ser melhorada

        #iniciar fase da abelha exploradora - só existe uma abelha exploradora na colmeia então ela so realiza uma ação no final de cada ciclo de forrageamento
        #primeiro deve se salvar a melhor abelha do ciclo de forrageamento
        if fitnessDaColonia[fitnessDaColonia.argmin()] < melhorFitness:
            melhorSolucao[:] = colonia[fitnessDaColonia.argmin()]
            melhorFitness = fitnessDaColonia[fitnessDaColonia.argmin()]
        #agora que a melhor solução da iteração foi salva verificamos se a solução de alguma abelha ultrapassou o numero limite de tentativas que elas tinham pra tentar evoluir
        if tentativas[tentativas.argmax()] >= numeroDeTentativas:
            #a função da abelha exploradora é encontrar um nova fonte de alimento para a abelha que ultrapassou seu numero de tentativas na colonia
            colonia[tentativas.argmax()] = np.random.permutation(D) #gera a nova solução
            fitnessDaColonia[tentativas.argmax()] = fitness(colonia[tentativas.argmax()],distancias) #gera o fitness dessa nova solução
            tentativas[tentativas.argmax()] = 0 #reseta o número de tentativas para a nova fonte de alimentos dessa abelha

        #print("Melhor Solucao e Melhor Fitness Atual")
        #print(melhorSolucao)
        #print(melhorFitness)

    melhoresSolucoes[r,:] = melhorSolucao
    melhoresFitness[r] = melhorFitness

print("Fim da Execução!")
for i in range(numeroDeExecucoes):
    print("execucao %d" % (i))
    print(melhoresSolucoes[i,:])
    print(melhoresFitness[i])
    print("-----------------------------")

Essa parte final serve para plotar em um gráfico o resultado gerado por meio do ABC:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#Plotando o resultado gerado pelo ABC
fig2, ax2 = plt.subplots()

for i, txt in enumerate(cidades):
    ax2.annotate(int(txt), (coordenadas_x[i], coordenadas_y[i]))

    plt.xlabel('Coordenadas X')
plt.ylabel('Coordenadas Y')
plt.title('Instância com 5 cidades')

melhorSolucao = np.append(melhorSolucao[:],melhorSolucao[0])    
plt.plot(coordenadas_x[melhorSolucao[:]],coordenadas_y[melhorSolucao[:]],coordenadas_x[melhorSolucao[:+1]],coordenadas_y[melhorSolucao[:+1]],'ro')
plt.show()

print("Roteiro de cidades percorridas pelo CV = %s" % str(melhorSolucao+1))
print("Distancia percorrida pelo CV = %f" % melhorFitness)

Se tiver alguma dúvida pode deixar ela nos comentários que responderei assim que puder!